Delaunay-Triangulation
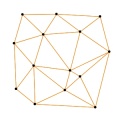
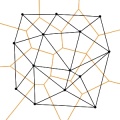
Die Delaunay-Triangulation (nach dem russischen Mathematiker Boris Nikolaevich Delone (frz.: Delaunay, 1890-1980), auch: Triangulierung) ist ein gebräuchliches Verfahren der industriellen Bildverarbeitung und Computergrafik, um aus einer Punktmenge ein Dreiecksnetz zu erstellen.
Grundlage der Triangulation nach Delaunay ist die Umkreisbedingung, wonach der Umkreis eines Dreiecks keine weiteren Punkte (der vorgegebenen Punktmenge) enthalten darf. Durch die Umkreisbedingung wird bei der Delaunay-Triangulation der kleinste Innenwinkel über alle Dreiecke maximiert. Für den Sonderfall, dass auf dem Umkreis mehr als drei Punkte liegen, ist die Delaunay-Triangulation nicht eindeutig. Im dreidimensionalen Raum wird statt der Umkreis- eine Umkugelbedingung verwendet.
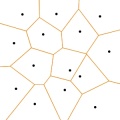
Die Delaunay-Triangulierung ist der duale Graph des Voronoi-Diagramms.
Literatur
- B. Delaunay: Sur la sphere vide. Bulletin of Academy of Sciences of the USSR, pages 793-800, 1934